The language of dynamic and interactive graphics

This blog post explores if and how the framework for the analysis of static graphics offered by Yuri Engelhardt in his PhD thesis, The language of graphics: A framework for the analysis of syntax and meaning in maps, charts and diagrams (2002), might be usefully extended to become applicable to dynamic and interactive graphics as well. This brief exploration will center on a discussion of one example of a dynamic graphic: Gapminder World.

When I read Engelhardt’s PhD thesis a short while ago, I was highly impressed by the analytic framework presented in it. The language of graphics tackles the subject of the syntactics of graphic objects. Roughly this means that it is concerned with the manner in which graphic objects combine into meaningful arrangements. Engelhardt’s framework allows an analyst to disentangle the jumbled mess of elements found in a given graphic and acquire a very firm and precise grasp of the manner in which the components of the graph combine to form a meaningful whole.

Engelhardt’s framework is intended to be applicable to a wide range of graphics including diagrams, maps, charts, graphs, tables and information visualizations, but it is emphatically not designed to extend to dynamic images. (( Initially Engelhardt claimed that his framework was suitable for the analysis of all images, as long as they were both flat and static (Engelhardt 2002: 7-8). However he seems to have taken to heart the criticisms of reviewers who praised the overall value of his work, but  questioned the framework’s ability to cope with highly iconic or mimetic signs (e.g. Forceville 2003, 2011). In an article published in 2007, Engelhardt states that his framework is not designed to cover either images of physical scenes or objects nor artistic images, but instead pertains to the range of images “often collectively referred to as “graphics” (Engelhardt 2007: 23). )) In 2002 Engelhardt wrote on this: “In the context of this thesis we decided to take one step at a time: We will first try to understand static versions of graphic representations, before we will try to understand dynamic and interactive versions” (Engelhardt 2002: 10). More than a decade has passed since then, during which the popularity of interactive and dynamic graphics has been expanding rapidly. Thus the time seems ripe to start thinking about that next step. Attempting to take that next step in this space of this blog post however would be overly ambitious. Instead this post aims to serve as a preparatory stretching of the legs, something that should surely be useful after a decade long standstill!

It would not be feasible to provide even an abbreviated summary of Engelhardt’s complete PhD thesis in the space of this blog post. Therefore I will try instead to demonstrate his framework’s functioning and power in the next section by discussing how it might be applied to Gapminder World.

Gapminder World, also known by the name “Wealth and Health of Nations”, is a dynamic and interactive graph that shows the development of countries since 1800 as captured in statistical data concerning factors such as life expectancy, fertility and income levels. If you are not familiar with the graphic I would heartily recommend taking a look at the spirited demonstrations of its use given by Hans Rosling, chairman and co-founder of the Gapminder Foundation, in a series of TED lectures (2 examples of which are embedded below).

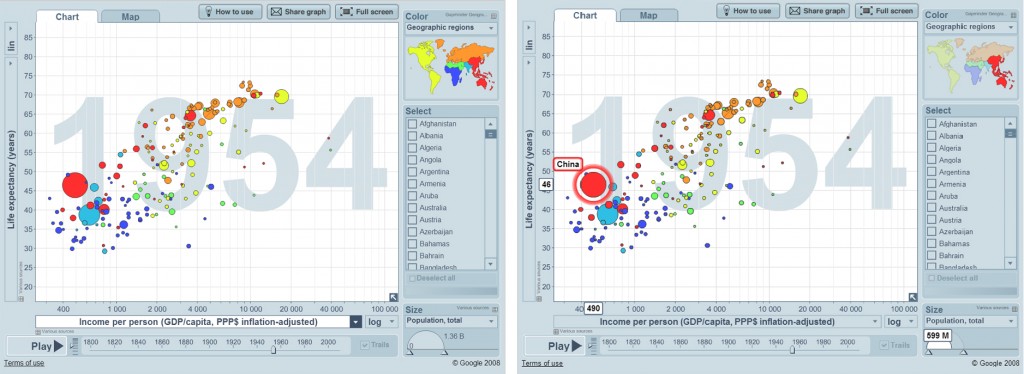
The screenshot in figure 1 displays the Gapminder World graph as it appears before the user has started interacting with it. Before we turn to the dynamic and interactive dimension of the graphic, let’s take a brief look at how the graphic in this static form might be described using the terminology introduced by Engelhardt in his 2002 book and a 2007 follow-up article. This way we can acquire a grasp of the functioning of Engelhardt’s framework and at the same time familiarize ourselves with the graphic.

Figure 1. Screenshot of “Gapminder World” / “The Wealth and Health of Nations” before any interactions have taken place.

According to the recursive definition proposed by Engelhardt, a graphic objects may consist of a graphic space (which may be meaningful) and graphic objects (which may themselves again consist of a graphic space and graphic object, etc.). In addition graphic objects are considered within Engelhardt’s framework to be carriers of visual attributes such as color, shape, and size. Within the framework, if a graphic consists of multiple graphic objects, it is considered to be a composite graphic object. The graph visible in figure 1 provides a clear example of a composite graphic object: it is made up of a number of graphic objects including a scatter plot (positioned on the left, covering the largest part of the figure) and a geographical map (positioned in the top right corner) both of these themselves again also consist of multiple graphic objects. On this first syntactic level the spatial arrangement of the graphic objects does not appear to bear any meaning. The spatial arrangement of graphic objects within the scatter plot and the geographic map however is meaningful. The map provides an example of a distorted metric space in which all ratios of spatial distances are meaningful. The scatter plot provides an example of a composite metric spaceconstructed out of a vertical and a horizontal axis in which the ratios in horizontal and vertical distances carry meaning: the position of a bubble on the horizontal axis provides an indication of the income level in the country that it represents, the position on the vertical axis does the same for the life expectancy. (( The map provides an example of what Engelhardt terms a meaningful physical space, the scatter plot provides an example of a meaningful conceptual space (2007: 31-34.) )) The bubbles placed on the scatter plot derive meaning from their placement along the two axis, but also from their size and color. The geographic map functions as a somewhat unusual legend object: it serves to identify the meaning that should be ascribed to the colors given to the bubbles placed on the scatter plot by portraying these countries in that same color on the map. (( The use of a map as a legend object diverges a little from the prototypical use of a legend object (which is usually attached to a map!), which according to Engelhardt consists of a table with symbols or objects with different visual attributes (e.g. different colors) in the first column and a designation of their meaning in the second (Engelhardt 2002: 195). )) Another legend object placed in the bottom right corner identifies the meaning of the size of the bubbles, which by default stands for the population total of the country the bubble represents.

We could go into further detail, but I hope that this brief analysis has sufficed to demonstrate the functioning and power of Engelhardt’s framework when applied to static graphs and has served to introduce the graphic.

An analysis in terms of graphic objects, their spatial arrangement and visual attributes (i.e. one of the sort just offered), I believe, can offer a complete grasp of the manner in which the components of a static graph combine into a meaningful whole (i.e. of the syntactics of a static graphic). If we want analyze dynamic or interactive graphics however there will be a number of additional elements that we will need to take into account. Starting off from the dynamic nature of animated graphs such as Gapminder World a first aspect that comes to mind as one that would need to be taken into account if one were to attempt to extend Engelhardt’s framework to cover dynamic and interactive graphs, I would suggest, is change.

Within a dynamic graph the visual attributes (again: shape, size, color, etc.) of graphic objects may alter as well as their spatial position. For an example, take a look at the brief video below, where I play around with Gapminder World a little. You will first see how I choose to have the colors of the bubbles stand for the average fertility rates for the countries they represent and then click play. What follows is a short animation that shows various bubbles move across a scatter plot, grow and shrink and change in color. On average you will see a tendency for the bubbles to move upwards and rightwards, grow in size and turn more blue, respectively indicating an increase in life expectancy, income levels and population sizes and a decrease in fertility rates.

A second element that needs to be considered when analyzing the syntactics of dynamic graphics might be termed arrangement in time. Graphic objects may be positioned in time in a manner that’s roughly analogous to the manner in which they are positioned in space. In a given graph order in time or ratios in “distances in time” may signify meaning, just as spatial relations may function to represent order or proportions. And just as spatial relations within a graphic may consist of both object-to-space relations and (spatial) object-to-object relations, so temporal relations may consist of both object-to-time relations and (temporal) object to object relations. What complicates matters further in the case of temporal relations however is that graphic changes (i.e. alterations of visual attributes such as size, color and movement of graphic objects through graphic space) may also be positioned in time.

A third element that would need to be taken into account if we were to develop a framework of the syntactics of dynamic and interactive graphics would be causal relations. When a user interacts with an element of an interactive graphic, for example by hovering over it with the mouse, clicking it, or by sliding a marker in a timebar slider, other elements on the screen will usually (also) display change. (( See Segel and Heer (2010)  for a discussion of timebar sliders and various other elements found in interactive graphics. )) When you, for example, hover over one of the bubbles located on the scatter plot in Gapminder World (e.g. China), a number of changes will occur (see figure 2).

Figure 2. Comparison of two screenshots of Gapminder World, showing the effect of a mouse over.

On the map in the top right corner the colors of all geographic regions will fade a little, except for the color of the geographic region where the country that is represented by the bubble, over which you hover your mouse, is located. Meanwhile on the legend object associated with the sizes of the bubbles, located in the bottom right corner, a semi circle will appear in front of another semi circle, indicating how the selected country’s population total compares to population total of the country with the largest population total. Moreover three different labels will appear: one on both axis and another close to the chosen bubble. The user will likely understand that all the graphic objects that have changed or even appeared this way (or in the case of the map, the one object conspicuously unaffected by change) are related to the object with which interaction took place. Cause-effect relations thus play a syntactic role here similar to one played in many static graphs by visual attributes (e.g. color) or spatial arrangements (e.g. spatial grouping).

The challenge would now be to analyze a diverse and wide corpus of dynamic and interactive graphics (as Engelhardt does in his 2002 book with static images) in order to compose a fine-grained taxonomy of possible syntactic relations that involve change, arrangement in time and cause-effect relations (again in the same manner Engelhardt does in his work). If well done, I believe such a framework should provide an useful tool that could be used to investigate the distinctions between different types of dynamic graphics and possibly even to help one to come up with new graphic forms, to offer more precise accounts of phenomena such as those described by Segel and Heer (2010) (e.g. consistent visual platform or detail or demand), or serve as the basis for a normative analysis. It’s a challenge that I aim to take up. More posts here may follow as I get further along. We’re done stretching, now let’s try to take that next step.

References

• Engelhardt, Yuri (2002). The language of graphics. A framework for the analysis of syntax and meaning in maps, charts and diagrams. Amsterdam: Institute for Logic, Language and Computation, University of Amsterdam.
• — (2007). ‘Syntactic structures in graphics.’ Image. Zeitschrift für Interdisziplinäre Bildwissenschaft. 5.1: Themenheft: Computational Visualistics and Picture Morphology: 23-35.
• Forceville, Charles (2003). Review of Yuri Engelhardt, The Language of Graphics: A Framework for the Analysis of Syntax and Meaning in Maps, Charts, and Diagrams (ILLC 2002). Document Design 4: 287-290.
• — (2011). ‘Practical cues for helping develop image and multimodal discourse scholarship.’ In: Klaus Sachs-Hombach and Rainer Totzke (eds.), Bilder, Sehen, Denken. ZumVerhältnis von begrifflich-philosophischen und empirisch-psychologischen Ansätzen in der bildwissenschaftlichen Forschung. Cologne: Von Halem, 33-51.
• Segel, Edward and Jeffrey Heer (2010) ‘Narrative visualization. Telling stories with data.’ IEEE Transactions on Visualization and Computer Graphics. 16.6: 1139-1148.